2. 湖南省佳和农牧股份有限公司, 长沙 410007
2. Hunan Jiahe Agriculture and Husbandry Inc.,Changsha 410007, China
畜禽饲料的研制是一项系统工程,其配方设计是一项核心技术。直到现在,饲料工业和畜禽养殖场有许多不同种类和生产用途畜禽的饲粮,采用不同目标函数、约束条件或数值算法的数学规划,通常是线性规划,进行计算机配方设计[1-18]。这类饲料配方设计是满足禽畜生存、生长和生产所需要各种养分的成本最低设计。在配方设计的过程中,逐次设计单个配方,以这种序列方式完成所有配方的设计。这种序列设计简单、实用、有效,是目前生产和科研中广泛采用的畜禽饲粮配合方法。不过,在有多个配方需要设计的情况下,如果采用这类序列设计,虽然每个配方都有可能获得最优的结果,但是这种最优配方从配方个体本身来看是最优的,从配方全体来看就不一定最优的。而且,序列设计不仅选择最优配方的范围小,而且浪费人力资源,增加计算成本[19]。因此,本文提出多配方平行设计配合畜禽饲粮。与传统的序列方法截然相反,平行设计及其算法能同时在不同处理设备上执行目标操作,最后合并而得到正确结果,它起源于计算机科学,逐渐扩大到信息技术与数值计算的广泛领域[20-21]。不言而喻,一个饲料加工企业或畜禽养殖单位,如果有若干个配方要进行设计,并有多种选择机会获得更好的最低成本的饲料配方,则需要进行多配方平行设计。本研究应用计算机多配方平行设计方法,探讨多种机会选择更好的最优畜禽饲料配方的可行性和应用前景。
1 材料与方法 1.1 畜禽饲料多配方平行设计的数学模型畜禽饲料配方设计是一个典型的组合优化问题,它是应用线性规划将若干种原料按一定比例组成满足特定营养要求和达到成本最低价格的配方。依此义,构建畜禽饲料多配方平行设计的数学模型,通过如下数学符号和公式表达。
设n为配方的个数,m为饲料原料的个数,Xij、Cij分别为配方i中饲料原料j的用量和单价,所考察的问题是通过线性规划的数学优化方法,使得总饲料成本 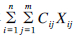
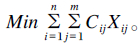
|
(式①) |
同时,式①的成立是在满足下列公式的条件下:
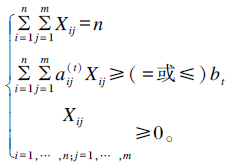
|
(式②) |
式中:n为正整数,n≥2;t为饲料养分的个数,t=1,…,p;aij(t)为配方i中饲料原料j的养分t的单位含量;bt为饲料养分t的最小或最大需要量。
1.2 饲料原料所用的饲料原料包括玉米、大麦、次粉、麦麸、豆粕、鱼粉(粗蛋白质含量63%)、豆油、葡萄糖、无水磷酸氢钙、石粉、食盐、DL-蛋氨酸(Met)、L-赖氨酸(Lys)、多维、一水硫酸锌、亚硒酸钠和无水硫酸铜。饲料原料的营养成分和含量来源于《中国饲料成分及营养价值表(2014年第25版)》[22-23],饲料价格数据大部分由湖南省佳和农牧股份有限公司提供,其余的参考阿里巴巴的网上交易价格[24]。表 1列出了主要原料的养分含量和价格。
|
|
表 1 多配方平行设计的生长猪饲粮主要原料的养分含量和价格 Table 1 Nutrient contents and prices of main ingredients of diets for growing pigs by parallel design with multiple-formulas |
本研究提出的猪饲料多配方平行设计,是指在同一数学模型中采用同样的优化方法同时配合若干个满足特定营养需要量和达到成本最低价格的配方。从数学的角度来说,进行最优配方设计的目的是找到1组非负变量的最优解,即自变量向量x=(x1,x2,…,xn)的成本函数最小值。也就是:
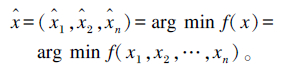
|
(式③) |
式中: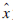
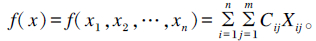
|
(式④) |
不难扩展,在一有n(≥2)个配方设计问题中,可根据畜禽群体的生长和生产实际情况的需要,分成几个小段,如k个,k=1,…,n。特别地,当k=1时,同时优化全部配方;当k=n时,则分n个点段同时进行配方优化。因此,n个配方问题可以有3种不同多配方平行设计的优化方案,即全段、小段和点段方案。也就是说,全段包括所有的配方,小段至少有2个配方,点段只有一个配方。本研究以生长猪饲料配方为例进行多配方平行设 计。全段配方包括所有7种不同生长阶段的饲 粮。小段配方有4种,即乳猪料、小猪料、中猪料、大猪料,分别含有2、2、2、1种饲粮。点段配方即是一点一段,每段有1种饲粮,共有7种,即为NRC(2012)建议的体重5~7 kg、7~11 kg、11~25 kg、25~50 kg、50~75 kg、75~100 kg和100~135 kg的生长猪饲粮,分别命名为教槽料、保育料、小猪前期料、小猪后期料、中猪前期料、中猪后期料和大猪料,依次用符号Gw05、Gw07、Gw11、Gw25、Gw50、Gw75和Gw100表示。
不难想到,如果生长猪饲粮配合的最优解存在,则全段配方的只有1个,点段配方的有7个,而小段配方的不仅只有6个,要根据组合理论进行配方间的搭配所获得的结果而确定。就本例而言,首先,将生长猪7种饲粮依次用7个不同数字(1、2、3、4、5、6、7)表示。接着,进行小段设计。若要形成小段,则至少需要2种不同饲粮,才符合如上小段的定义。于是,从7种配方或7个不同数字中取出2个进行两两搭配,形成21种不同组合或小段;再将其分成7组,组号分别为Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ和Ⅶ。最后,将每组小段的6个配方与剩余1个点段配方结合,完成多配方平行设计,其结果列入表 2。由此可见,7种生长猪饲粮的每种可有7个配方及其最优解,总共可获得49个配方的最优解,从而值得作进一步的考察。
|
|
表 2 多配方平行设计的7种生长猪饲粮的搭配组合 Table 2 Matched combinations of 7 diets for growing pigs by parallel design with multiple-formulas |
营养标准是不同猪群饲粮养分的需要量,也是饲料配方设计的标准。根据美国国家研究委员会(NRC)猪营养需要委员会的《猪的营养需要》最新版本第11版[25-26]提出的营养需要量,确定本次多配方平行设计的营养学标准。7种配方所用的饲料营养成分、约束条件、需要量和单位列于表 3。所列的猪饲粮养分需要量即配方设计的标准共27项。值得提出,新版列出了2项新的重要营养标准指标标准全肠道可消化磷(STTDP)和总氮(TN)。计算公式如下:

|
(式⑤) |
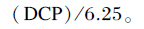
|
(式⑥) |
式中:STTD数值参考文献[25]。
|
|
表 3 多配方平行设计的生长猪饲粮营养标准 Table 3 Nutritional standards of diets for growing pigs by parallel design with multiple-formula |
猪饲粮多配方平行设计的数值计算,使用GAMS 23.5软件[27]。GAMS的全称是General Algebraic Modeling System,是美国出品的一款国际知名的数学规划和优化的高级建模系统。一个标准的GAMS程序由集(sets)、参数(parameters)、变量和方程(variables and equations)模型和解(model and solve)、结果输出(display)组成。根据GAMS程序的语言和语法规则,按照上述的GAMS程序结构,利用饲料原料的价格和营养值及饲粮饲养标准,编写了猪饲粮的全段、小段和点段这3种多配方平行设计的GAMS程序,运行后获得了所有配方的最低成本和满足不同生长猪群饲粮营养需要的结果。
1.6 定量比较的方法为了定量分析饲粮配方养分的拟合程度,定义配方养分的计算值与其标准值的离差平均值。计算公式如下:
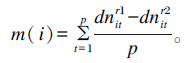
|
(式⑦) |
式中:p为饲粮或配方养分的个数;t为饲粮i中养分t;r为生长阶段;dnitr1为阶段r中饲粮i的养分t的含量计算值;dnitr2为阶段r中饲粮i的养分t的含量标准值;m(i)为阶段r中饲粮i的养分t的含量计算值与其标准值的离差平均值。
如果饲粮配方最优解存在,可行解就一定存在。这就意味着离差平均值只有大于或等于0的值。这个离差平均值,若等于0,则表明养分的配合值与标准值相等,也就是该养分达到了营养标准值;若大于0,则表明饲粮养分的配合值大于或等于标准值;它越大,就表明所配饲粮养分含量整体距离标准值的差异性大,反之就小;它异常大,则可能配方中有养分极端值。因此,这个离差平均值能客观评价多配方平行设计饲粮养分配合值的适合度。
2 结果与分析 2.1 饲粮配方原料用量的比较与分析多配方平行设计配合的7种不同阶段生长猪群的饲粮教槽料、保育料、小猪前期料、小猪后期料、中猪前期料、中猪后期料和大猪料,其原料用量列在表 4。由于采用分组的小段多配方平行设计,每种饲粮有7个配方,总共有49个配方,其中组内配方相同的28个,组内配方不相同的21个。这些配方所拟配16种饲料原料中,硫酸铜没有进入饲粮配合,所有配方中的使用量均为0(表中未列);葡萄糖的用量,仅乳猪教槽料使用5%,为限配所致。由表 4可见,体重5~7 kg的7个教槽料的原料用量和种类完全一样;体重7~11 kg的7个保育料的原料种类一样,用量不完全一样,仅在亚硒酸钠用量的不相同;体重11~25 kg的7个小猪前期料、25~50 kg的7个小猪后期料、50~75 kg的7个中猪前期料、75~100 kg的7个中猪后期料和100~135 kg的7个大猪料的原料用量都存在差别。高能量饲料原料,包括玉米、豆粕、鱼粉和豆油,7种饲粮的平均用量依次为91.9%、94.1%、91.3%、90.2%、88.9%、79.2%和83.9%;高蛋白质饲料原料,包括豆粕和鱼粉,7种饲粮的平均用量依次为40.9%、34.1%、34.5%、25.2%、23.5%、14.2%和18.9%。
|
|
表 4 多配方平行设计的生长猪饲粮原料用量和成本 Table 4 Ingredient consumption and diet cost for growing pigs by parallel design with multiple-formulas |
综合来看,7种饲粮配方的成本大小,从教槽料到大猪料依次减小,平均成本价格依次是4.153、4.059、3.837、3.795、3.622、3.598和3.597元/kg。结合配方原料的用量来看,饲粮内的同价同量,即饲粮内同一价格的配方,其原料用量一样;饲粮间的同价不同量,即饲粮间同一价格的配方,其原料用量不一样;再者,总的来看,高能量和高蛋白质饲料原料的用量随着其成本价格下降而减小。
2.3 饲粮配方养分含量的比较与分析多配方平行设计配合的7种不同阶段生长猪的饲粮教槽料、保育料、小猪前期料、小猪后期料、中猪前期料、中猪后期料和大猪料的养分含量列在表 5。和营养标准(表 3)比较,这些饲粮配方的养分消化能(DE)、代谢能(ME)、钙(Ca)、TP、STTDP、精氨酸(Arg)、组氨酸(His)、异亮氨酸(Ile)、亮氨酸(Leu)、Lys、Met、Met+半胱氨酸(Cys)、苯丙氨酸(Phe)、Phe+酪氨酸(Tyr)、苏氨酸(Thr)、色氨酸(Trp)、缬氨酸(Val)和TN、钠(Na)、氯(Cl)、镁(Mg)、钾(K)、铁(Fe)、锰(Mn)、铜(Cu)、锌(Zn)和硒(Se),都达到或超过标准营养需要量[NRC(2012)]。虽然这些饲粮配方中的养分含量都达了满足生长猪的饲粮养分需要量的标准,但是达标的程度不一样。在表 6中,列出了7组共49个饲粮配方养分含量与其标准值(即最小需要量)的离差平均值,每组有7种配方饲粮,即教槽料、保育料、小猪前期料、小猪后期料、中猪前期料、中猪后期料和大猪料。Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ和Ⅶ组养分含量离差平均值如表 6的极差(最大值,最小值),分别是(1.69,1.69)、(3.71,1.42)、(10.19,1.65)、(11.96,2.58)、(20.38,2.53)、(12.74,3.00)、(12.24,3.05),亦即0、2.29、8.54、9.38、17.84、9.74、9.19。离差平均值大,距离标准值的程度高;离差平均值的极差大,表明差异范围广。综合比较发现,养分含量的离差平均值及其极差依次是:Ⅴ组>Ⅵ组>Ⅳ组>Ⅶ组>Ⅲ组>Ⅱ组>Ⅰ组。出现养分含量的离差平均值及其极差大,很可能是配方内存在大的养分极端值造成的。根据离差平均值提供的信息,检查发现:Ⅰ组没有较大的硒含量值,Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ和Ⅶ组有大的硒含量值。值得注意的是:配方设计所拟配的原料硫酸铜没有被利用,无养分含量值,表明它不必要参加饲粮配合,利用有机生物饲料的铜就可以满足饲粮铜的需要量。
|
|
表 5 多配方平行设计的生长猪饲粮的养分含量 Table 5 Nutrient contents of diets for growing pigs by parallel design with multiple-formulas |
|
|
表 6 多配方平行设计的生长猪饲粮养分含量的离差平均值 Table 6 Means of nutrient level deviations from requirements for growing pig rations by parallel design with multiple-formula |
平行设计是一种同时间处理若干不同对象的并联设计与算法[19-20]。以生长猪的饲粮配合为例,本研究提出畜禽的多配方平行设计与算法。它的特点有如下3点:第一是多配方性。它能够使若干个配方参加设计,并能够找到这若干个配方的最优解,如果它们都有可行解的话。小段设计是找到某饲粮的多个配方的途径。一方面通过专业性分段(如生长阶段)找到多配方的组合;另一方面按照数学的组合理论进行饲粮间的相互搭配找到若干个配方的组合。第二是并行性。所谓并行性就是这若干个配方同时处在一个最优化过程。某一个配方的最优解,不是它本身决定,而是由这若干个配方相互决定。但是,这与配方设计方法有关。如果这若干个配方分成几段,那么段内配方受到影响,段间配方不受影响,因为分段的目的使其中某几个配方不受其他配方的影响。如果把这若干个配方分成1段1个配方,那么它们每个配方之间就相互不受到影响,彼此独立。本文提出的点段配方设计方法,由于配方间的相互独立性,实质上能够获得与序列法一样的配方结果。或者说,在研究多配方平行设计的同时,也可以把常用的独立配方法同时加以比较。第三是解的全局性。如果进行多配方平行设计,把若干个配方同时加以考察,那么在可行解的基础上获得的最优解就是它们的共同解,即满足所有配方的全局最优解。
3.2 关于饲粮养分矿物质的配合饲粮养分矿物质包括常量和微量元素,特别是微量元素,由于生物有机饲料的含量较低,往往不能满足饲粮的最低需要量,需要用矿物质饲料加以补充。本研究选择3种矿物质饲料亚硒酸钠、硫酸锌和硫酸铜参加配方设计,前述的矿物质比较与分析表明,所有饲粮养分锌和部分养分硒达不到饲粮的需要量,而且不同配方缺少的量也不一样。针对不同情况,用亚硒酸钠、硫酸锌作了补充(表 4),而不是用某种预混料进行统一的添加。值得指出,亚硒酸钠的补充,使得在配方中出现了个别配方的养分含量极端值。这种极端值即是距离营养标准值较远,超过需要量较多,是由于硒、锌元素在其化合物中的含量高,而配方的添加量非常小而造成的,但可通过人工或非人工的方法校正到需要量或适当高于需要量的用量。本文作出这样的分析,是为应用者提供信息。Ferket等[28]曾经指出,很多生产者饲喂饲粮锌、铜的添加量高出NRC(2012)建议量许多,多达超过NRC建议量的10倍,直接的结果是环境负担加重,动物的生长改善并不理想。Powers等[29]也曾提出畜禽营养策略要能够应对环境的挑战。
3.3 关于饲粮配合方法目前,畜禽饲料配方设计采用序列法,一次一个配合满足饲粮能量、钙、磷和粗蛋白质需要,或者再加入氨基酸约束条件的最低成本饲粮。本研究多配方平行设计方法配合的生长猪饲粮,不仅其养分,包括能量、钙、磷、粗蛋白质、氨基酸、矿物质等,都达到或超过营养标准的需要量,而且其成本价格也是最低的。有4点值得指出。第一是饲料原料的选择。本配方设计拟配的饲料共16种,多数是基于湖南省佳和农牧股份有限公司猪生产中使用的原料(表 1)。其中硫酸铜没有被利用,无养分含量值,表明它不必要参加饲粮配合,利用有机生物饲料的铜就可以满足饲粮铜的需要量。第二是养分项目的选择。美国NRC《猪的营养需要》第11版(2012)[25-26]列出的能量、钙、磷、粗蛋白质、氨基酸和矿物质等共27个养分项目都纳入到本配方设计中,其中2个养分STTDP和TN是该书中首次提出的,也被作为约束条件纳入数学模型中。第三是预混料的选择。预混料主要是补充微量矿物质、维生素、Met和Lys。由于矿物质、Met和Lys作为养分约束项目添加在配方模型中,故配方设计中预混料没有配置,而是用多维代替。第四是关于饲粮维生素配合。NRC的《猪的营养需要》第11版(2012)[25-26]列出了生长猪不同阶段的维生素需要量,但是本研究多配方平行设计没有考虑,作为约束条件纳入数学模型中。因为目前饲料成分及营养价值表中的维生素含量部分有许多缺项,没有可利用的数据,可行解无法获得。通过多次饲粮试配不满足需要量的维生素种类和数量已经获得,以维生素添加剂方式补充到饲粮中,达到符合饲粮维生素需要量的目的。
3.4 关于饲粮配方选择方法首先,选择饲粮配方要有科学依据,要考虑饲粮的低价性、充足性、平衡性和安全性。养殖业是一个高度竞争性行业,利润空间相对小。在此情况下生产,经济效益是确保长期盈利能力的关键因素,经济问题成了众多关注问题中的唯一基础[2]。因此,畜禽饲粮配合把最低成本作为目标函数,并把NRC(2012)提出的生长猪营养需要的推荐量作为养分约束条件,使得饲粮配方的低价性、充足性、平衡性和安全性有了科学的理论基础和广泛的实际背景。本研究以生长猪饲料配方为例进行多配方平行设计,通过16种饲料原料的搭配和7种不同生长阶段的配方组合,获得的49个配方都是成本最低的,其能量、钙、磷、粗蛋白质、氨基酸、TN和矿物质的含量都达到或超过能满足其生存和生长的营养需要,个别配方的硒添加量给予适当减少,饲粮的安全性增强,成本也会降低。
其次,要有能产生多配方的饲粮配合方法。本文提出的多配方平行设计是选择最佳配方的一种新途径,它选择配方的范围非常广。例如,本研究有7种饲粮参加多配方平行设计,全段和点段各有1次设计,每次都产生7个饲粮。小段设计的次数和产生的饲粮配方数目非常多。譬如,本研究的生长猪的7种饲粮配合,由于采用小段设计的组合,产生的49个饲粮配方是传统的序列设计的7倍。由此例看来,多配方平行设计是从众多可选择的最低成本饲粮配方中选择满足养分充足性、平衡性、安全性和低价性的饲粮配方的一种好途径。
4 结 论① 本研究提出的畜禽饲粮多配方平行设计是另一类配方设计,是通过不同的多配方组合同时产生不同的多个饲粮配方;不仅提高了配方设计的效率,而且更重要的是增加了选择更好饲粮配方的机会,为获得畜禽的合理和平衡饲粮提供了新途径。丰富的实例验证了多配方平行设计应用于动物饲料配方设计的实际可行性。
② 通过多配方平行设计的2种不同设计方案小段和点段的搭配组合,获得7组、共49个生长猪饲粮配方。经过饲粮原料用量、单位价格和养分含量的比较与分析,这些配方的饲粮能量、钙、磷、粗蛋白质、氨基酸、TN和矿物质等的含量,都达到或超过NRC(2012)提出的生长猪营养需要的推荐量,也满足最低成本的要求。本研究只是提出用平行设计和组合理论配合畜禽饲粮及探讨其可行性,进一步的研究是对这些方法和理论进行深层次的探讨,同时把畜禽饲粮多配方平行设计方法应用到养殖企业和饲料加工厂的生产中。
| [1] |
PESTI G M, MILLER B R, CAREY C A. Proportionality among nutrients in least cost feed formulation[J].
Poultry Science, 1985, 64(5): 824–831.
( 0) 0)
|
| [2] |
LARA P, ROMERO C. Relaxation of nutrient requirements on livestock rations through interactive multigoal programming[J].
Agricultural Systems, 1994, 45(4): 443–453.
( 0) 0)
|
| [3] |
TOZER P R, STOKES J R. A multi-objective programming approach to feed ration balancing and nutrient management[J].
Agricultural Systems, 2001, 67(3): 201–215.
( 0) 0)
|
| [4] |
ZHANG F, ROUSH W B. Multiple-objective (goal) programming model for feed formulation:an example for reducing nutrient variation[J].
Poultry Science, 2002, 81(2): 182–192.
( 0) 0)
|
| [5] |
TUITOEK K, YOUNG L G, DE LANGE C F, et al. The effect of reducing excess dietary amino acids on growing-finishing pig performance:an elevation of the ideal protein concept[J].
Journal of Animal Science, 1997, 75(6): 1575–1583.
( 0) 0)
|
| [6] |
CASTRODEZA C, LARA P, PEÑA T. Multicriteria fractional model for feed formulation:economic,nutritional and environmental criteria[J].
Agricultural Systems, 2005, 86(1): 76–96.
( 0) 0)
|
| [7] |
GUEVARA V R. Use of nonlinear programming to optimize performance response to energy density in broiler feed formulation[J].
Poultry Science, 2004, 83(2): 147–151.
( 0) 0)
|
| [8] |
PADEL S, SUNDRUM A. How can we achieve 100% organic diets for pigs and poultry?[J].
Aspects of Applied Biology, 2006(79): 237–241.
( 0) 0)
|
| [9] |
孙文志, 张忠远. 考虑养分变异性的最低成本饲料配方模型[J].
动物营养学报, 1996, 8(3): 31–37.
( 0) 0)
|
| [10] |
张元跃. 采用随机规划法进行饲料配方设计[J].
湖南农业大学学报, 1997, 23(1): 58–62.
( 0) 0)
|
| [11] |
黄汉英, 熊先安, 魏明新. 几种规划在优化饲料配方设计中的比较[J].
粮食与饲料工业, 1999(10): 26–27.
( 0) 0)
|
| [12] |
黄汉英, 熊先安, 魏明新. 模糊线性规划在优化饲料配方软件中的应用[J].
农业工程学报, 2000, 16(3): 107–110.
( 0) 0)
|
| [13] |
刘素华, 侯惠芳. 基于遗传算法的饲料配方设计[J].
计算机工程与应用, 2005, 41(7): 206–208.
( 0) 0)
|
| [14] |
艾景军, 刘大有, 曹东军, 等. 模糊线性规划饲料配方模型的建立与应用[J].
电子学报, 2001, 29(11): 1568–1570.
( 0) 0)
|
| [15] |
陈世希, 李翠华, 王渊源. 饲料配方设计的模拟退火优化策略[J].
厦门大学学报:自然科学版, 2001, 40(6): 1319–1323.
( 0) 0)
|
| [16] |
熊本海, 罗清尧, 庞之洪. 对偶模型在畜禽饲料配方优化设计上的应用[J].
中国农业科学, 2003, 36(11): 1347–1351.
( 0) 0)
|
| [17] |
朱犁, 孙玲. 随机规划与线性规划在饲料配方中的应用比较[J].
安徽农业科学, 2006, 34(9): 1778–1779.
( 0) 0)
|
| [18] |
张元跃. 一种新的饲料配方技术——杂种遗传算法[J].
动物营养学报, 2009, 21(5): 703–710.
( 0) 0)
|
| [19] |
WIKIPEDIA.Parallel algorithm[EB/OL].[2015-10-26].https://en.wikipedia.org/wiki/Parallel_algorithm#cite_note-1.
( 0) 0)
|
| [20] |
SMITH J R.
The design and analysis of parallel algorithms[M]. New York: Oxford University Press, 1993 .
( 0) 0)
|
| [21] |
WIKIPEDIA.Parallel computing [EB/OL].[2015-10-26].https://en.wikipedia.org/wiki/Parallel_computing.
( 0) 0)
|
| [22] |
熊本海, 庞之洪, 赵峰, 等. 中国饲料成分及营养价值表(2014年第25版)制订说明[J].
中国饲料, 2014(21): 29–39.
( 0) 0)
|
| [23] |
熊本海, 庞之洪, 赵峰, 等. 中国饲料成分及营养价值表(2014年第25版)(续)[J].
中国饲料, 2014(22): 37–42.
( 0) 0)
|
| [24] |
阿里巴巴.各种饲料原料价格[EB/OL].[2015-10-26].http://www.1688.com/jiage/-B8F7D6D6CBC7C1CFD4ADC1CF.html.
( 0) 0)
|
| [25] |
NRC.Nutrient requirements of swine[S].11th ed.Washington,D.C.:National Academy of Sciences,2012.
( 0) 0)
|
| [26] |
美国国家科学院科学研究委员会.猪营养需要[M].印遇龙,阳成波,敖志刚,译.北京:科学出版社,2014.
( 0) 0)
|
| [27] |
ROSENTHAL R E.
GAMS-a user's guide[M]. Washington,DC,USA: GAMS Development Corporation, 2010 .
( 0) 0)
|
| [28] |
FERKET P R, VAN HEUGTEN E, VAN KEMPEN T A T G, et al. Nutritional strategies to reduce environmental emissions from nonruminants[J].
Journal of Animal Science, 2002, 80: E168–E182.
( 0) 0)
|
| [29] |
POWERS W, ANGEL R. A review of the capacity for nutritional strategies to address environmental challenges in poultry production[J].
Poultry Science, 2008, 87(10): 1929–1938.
( 0) 0)
|




