2. 光明牧业有限公司, 上海 200436
2. Guangming Animal Husbandry Co., Ltd., Shanghai 200436, China
泌乳曲线是用来描述奶牛泌乳期内产奶量、乳脂率、乳蛋白率等性状随泌乳时间变化而变化的曲线。泌乳曲线模型在奶牛生产中有较强的指导意义,它除了能够提供个体动物的泌乳模型,还可以进行单体动物泌乳期和群体动物泌乳期的比较,甚至在动物出现某种临床型疾病之前就可以进行判定,从而对奶牛产奶量预测、遗传潜力估计、选种等方面起到重要的作用。自Gains[1]首次使用数学模型描述了泌乳期内产奶量与泌乳天数之间的函数关系以来,国际上陆续开展了泌乳曲线的数学模型的研究。典型的泌乳曲线模型有Wood不完全伽玛函数模型(简称Wood模型)、Wilmink(WIL)模型、逆多项式(IQP)模型、Ali-Schaeffer(AS)模型等[2-5]。如Da Cunha等[6]分别使用并比较了Wood模型、Wilmenk模型及Dijkstra模型这3种模型的拟合效果。Marek等[7]比较了7种泌乳曲线模型拟合的优势,结果表明Wood模型、Nelder模型和Marek-Zelinkova模型的拟合效果较好。国内也有研究者使用以上模型对奶牛泌乳曲线进行了大量研究,赵智华等[8]、毛永江等[9]、努尔比亚·吾布力等[10]分别研究了不同模型拟合中国荷斯坦奶牛的泌乳曲线。对于乳脂率和乳蛋白率等乳成分指标而言,目前可用于描述其变化的模型并不多,且研究的结果差异较大。
本研究拟采用Wood模型对上海奶牛育种中心有限公司长三角地区10个牛场的中国荷斯坦牛产奶量、乳脂率、乳蛋白率及乳中体细胞评分(somatic cell score, SCS)这4个主要的泌乳性状的变化曲线进行拟合,定量地描述其变化趋势,为中国荷斯坦牛的生产管理及主要泌乳性状的预测提供科学依据。
1 材料与方法 1.1 数据来源数据来源为长三角地区10个牧场2014—2016年1~3胎中国荷斯坦牛共123 765条奶牛性能测定体系(DHI)测定日记录(每个月记录1次),由上海奶牛育种中心有限公司提供。为保证分析结果的可靠性,对不完整的数据不进行分析,同时剔出了极端异常的产奶量及乳成分数据,对DHI测定数据进行的限定如下:泌乳时间为产后7~336 d,产奶量为5~60 kg,乳脂率为2%~7%,乳蛋白率为2%~6%,乳中体细胞数(somatic cell count,SCC)为1~5×106个/mL。考虑乳中SCC呈偏态分布,用如下公式转化为SCS[11]:
SCS=log2SCC/100+3。
最后符合条件的数据共104 368条。数据基本情况见表 1。
|
|
表 1 数据基本情况(平均值±标准差) Table 1 Details of analyzed data (mean±SD) |
用Wood不完全伽玛函数对产奶量、乳脂率、乳蛋白率和乳中SCS 4个指标的变化进行拟合,基本模型如下[12]:
Yt=atbect。
式中:t为泌乳周数;Yt为t时间的产奶量、乳脂率、乳蛋白率或乳中SCS;a、b、c为模型参数:a为产犊后的初始产奶量、乳脂率、乳蛋白率和SCS;b为达到峰值的倾斜度参数;c为下降的倾斜度参数。当参数b为正值,c为负值时,该模型可用于产奶量的拟合分析;当参数b为负值,c为正值时,该模型适合于拟合乳脂率、乳蛋白率和乳中SCS的拟合分析。在进行曲线拟合时,各参数初始值的确定采用Oloria等[13]计算所得的结果,并利用如下公式换算出以下二级参数:
Tmax=b/c;
Tmin=b/c;
Ymax=a(b/c)be-b;
Ymin=a(b/c)-beb;
Per=-(b+1)lnc。
式中:Tmax为在拟合产奶量时达到产奶量高峰所需的时间,即产奶量高峰出现时间;Tmin为拟合乳脂率、乳蛋白率和乳中SCS时,该指标达最低值的时间;Ymax为高峰产奶量;Ymin为乳脂率、乳蛋白率和乳中SCS的最低值;Per为泌乳持久力。
1.3 数据分析考虑到胎次对拟合效果影响较大,故对不同胎次数据分别进行拟合。所有产奶量数据均先用Excel 2010初步整理,再用Mtalab软件进行拟合,拟合效果用拟合度(R2)和均方误差进行评价。
2 结果 2.1 产奶量、乳脂率、乳蛋白率和SCS变化曲线的基本特征用Wood模型拟合1、2、3胎中国荷斯坦牛产奶量、乳脂率、乳蛋白率和乳中SCS变化曲线分别见图 1、图 2、图 3。从图中可以看出,测定日产奶量曲线为标准泌乳曲线,泌乳曲线均呈现先上升后较缓慢下降的变化趋势;而乳脂率、乳蛋白率及乳中SCS变化曲线则相反,呈现开口向上的倒抛物线变化,从最高点逐渐下降至最低点后又都具有逐渐上升的趋势。
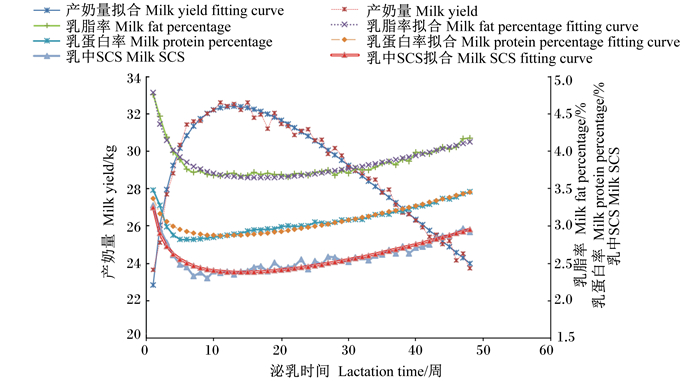
|
图 1 Wood模型对1胎奶牛产奶量、乳脂率、乳蛋白率及乳中SCS的拟合曲线 Figure 1 Fitting curves of milk yield, milk fat percentage, milk protein percentage and milk SCS for first parity daiy cows by Wood's model |
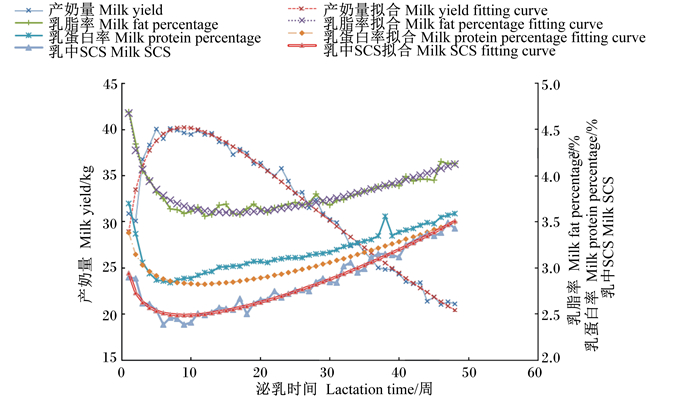
|
图 2 Wood模型对2胎奶牛产奶量、乳脂率、乳蛋白率及乳中SCS的拟合曲线 Figure 2 Fitting curves of milk yield, milk fat percentage, milk protein percentage and milk SCS for second parity daiy cows by Wood's model |
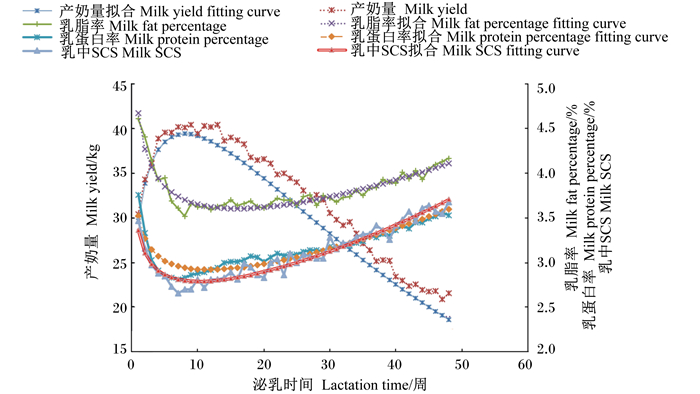
|
图 3 Wood模型对3胎奶牛产奶量、乳脂率、乳蛋白率及乳中SCS的拟合曲线 Figure 3 Fitting curves of milk yield, milk fat percentage, milk protein percentage and milk SCS for third parity daiy cows by Wood's model |
不同胎次产奶量、乳脂率、乳蛋白率和SCS变化曲线拟合参数、拟合度及均方误差见表 2。从表 2可知,产奶量曲线的拟合准确性最高,各胎次的拟合度均在0.98以上。乳中SCS曲线的拟合准确性其次,各胎次的拟合度均在0.93以上。比较不同胎次乳脂率泌乳曲线拟合度可知,1和2胎较高,均为0.96,3胎较低,为0.92。不同胎次的乳蛋白率泌乳曲线拟合度也均高于0.88。
|
|
表 2 不同胎次产奶量、乳脂率和乳蛋白率Wood模型拟合参数及拟合度 Table 2 The fitness and parameters for lactation curve of milk yield, milk fat percentage and milk protein percentage with Wood's model |
从各胎次拟合曲线图和二级参数可以看出,对于产奶量而言,1胎到产奶量高峰出现时间最晚,高峰产奶量也最低,但持续力最强,2和3胎到产奶量高峰出现时间分别为8.95和8.04周,高峰产奶量也较高,但持续力也较低。对于乳脂率而言,2胎乳脂率最先达到最低点;对于乳蛋白率而言,1、2、3胎均在11周左右达到最低点,且各胎次的乳蛋白率持续力基本相当;对于SCS而言,1胎到达最低值的时间最晚,2胎到达最低值的时间最早。
3 讨论 3.1 不同胎次荷斯坦牛泌乳曲线拟合效果的比较分析本研究发现,1胎产奶量高峰出现时间为12.92周(90 d),2、3胎分别为8.95(63 d)和8.04周(56 d),与毛永江等[14]报道的1、2、3胎的产奶量高峰出现时间分别为9.9(70 d)、7.4(58 d)和7.6周(53 d)基本一致,1胎的产奶量高峰出现时间延后,但与熊本海等[15]报道的中国北方荷斯坦奶牛1、2、3胎的产奶量高峰出现时间分别为67、30、33 d相比均滞后,导致这种差异的原因可能是熊本海等[15]研究中所采用饲养环境及测定产奶量的频率较多,而本研究中长三角地区奶牛是采用1个月记录1次泌乳数据的方案,泌乳高峰到来之前,可能没有泌乳数据记录,或者只有1次数据记录,预测产奶量高峰出现时间相对就可能延后。另外,就泌乳持续力分析,1胎的泌乳持续力为4.98,均高于2和3胎,这与Friggens等[16]报道的结果一致。另外,对于产奶量而言,1、2、3胎的拟合度均在0.98以上,说明Wood模型对于产奶量有很好的拟合效果。
3.2 不同胎次荷斯坦奶牛乳脂率曲线拟合效果的比较分析比较不同胎次乳脂率泌乳曲线拟合度可知,1和2胎高(均为0.96),3胎低(0.92)。这说明用Wood模型对乳脂率进行预测时,1和2胎较准确,3胎相对较差。且2胎乳脂率最先达到最低点(15.65周),而1胎乳脂率最后达到(16.47周),3胎居中。这与张美荣等[17]和罗清尧等[18]研究结果相似。这说明1胎乳脂率变化相对较小,用Wood模型进行曲线拟合效果相对较好,而2胎乳脂率变化相对较大,故准确性稍差。但总体来说,本研究各胎次拟合度均在0.90以上,可以用于中国荷斯坦牛乳脂率变化趋势的预测分析。
3.3 不同胎次荷斯坦奶牛乳蛋白率曲线拟合效果的比较分析比较不同胎次乳蛋白泌乳曲线拟合度可知:1胎最高(0.93),其次是2胎(0.90),3胎最低(0.88)。这说明用Wood模型对乳蛋白率进行预测时,1胎最准确,其次为2胎,3胎最差。且2胎乳蛋白率最先达到最低点(11.33周),而3胎乳蛋白率最后达到最低点(11.59周)。本研究获得的乳蛋白率拟合曲线均呈现先降低后升高的趋势,即泌乳初期较高,随后逐渐下降,随后逐渐上升,这与Steri等[19]研究的描述乳蛋白率变化曲线的规律基本相似。各胎次均在11周左右达到最低点,这与熊本海等[15]报道的乳蛋白率在6~8周达到最低点存在差异,可能是由于奶牛在不同的饲养环境下,饲喂管理方面的不同造成的。
3.4 不同胎次荷斯坦奶牛乳中SCS曲线拟合效果的比较分析比较不同胎次乳中SCS曲线拟合度可知,各胎次均大于0.93,且均方误差较小,特别是2胎的拟合度最高, 为0.97,这与Gołębiewski等[20]和毛永江等[14]的研究不一致,他们的研究结果表明, Wood模型不适宜用来拟合乳中SCS和SCC的变化规律,这可能与本研究所采用实际生产所取得的大样本统计有关,更适合用Wood模型进行拟合。
4 结论① Wood模型能极好地拟合中国荷斯坦奶牛的泌乳曲线,并较好地拟合乳中SCS、乳蛋白率和乳脂率曲线。
② 产奶量曲线为标准的泌乳曲线,而乳脂率、乳蛋白率和SCS变化曲线则为倒抛物线形。
| [1] |
GAINES W L. Persistency of lactation in dairy cows[M]. [S. l. ]: [s. n. ], 1927.
|
| [2] |
WOOD P D P. Algebraic model of the lactation curve in cattle[J]. Nature, 1967, 216(5111): 164-165. DOI:10.1038/216164a0 |
| [3] |
WILMINK J B M. Adjustment of test day milk, fat and protein yield for age, season and stage of lactation[J]. Livestock Production Science, 1987, 16(4): 335-348. DOI:10.1016/0301-6226(87)90003-0 |
| [4] |
NELDER J A. Inverse polynomials, a useful group of multifactor response fuctions[J]. Biometrics, 1966, 22(1): 128-141. DOI:10.2307/2528220 |
| [5] |
ALI T E, SCHAEFFER L R. Accounting for covariance among test day milk yields in dairy cow[J]. Canadian Journal of Animal Science, 1987, 67(3): 637-644. DOI:10.4141/cjas87-067 |
| [6] |
DA CUNHA D D N F V, PEREIRA J C, CAMPOS O F, et al. Selection of models of lactation curves to use in milk production simulation systems[J]. Revista Brasileira de Zootecnia, 2010, 39(4): 891-902. DOI:10.1590/S1516-35982010000400026 |
| [7] |
MAREK J, RAJMON R, HALOUN T. Critical evaluation of seven lactation curve estimation models[C]//ABRAHAM A, JIANG X, SNÁŠEL V, et al. Intelligent data analysis and applications. Cham: Springer, 2015: 73-84.
|
| [8] |
赵智华, 彭顺清, 李凤翔, 等. 用Wood模型拟合四川地区黑白花奶牛泌乳曲线的研究[J]. 四川畜牧兽医, 2000, 27(1S): 19-20. |
| [9] |
毛永江, 张亚琴, 许兆君, 等. 中国荷斯坦牛泌乳曲线拟合研究[J]. 畜牧兽医学报, 2011, 42(9): 1239-1248. |
| [10] |
努尔比亚·吾布力, 付雪峰, 热西提·阿不都热依木, 等. 新疆农七师荷斯坦牛不同模型泌乳曲线拟合效果分析[J]. 中国奶牛, 2012(17): 19-22. DOI:10.3969/j.issn.1004-4264.2012.17.006 |
| [11] |
POLOTT G E. Deconstructing milk yield and composition during lactation using biologically based lactation models[J]. Journal of Dairy Science, 2004, 87(8): 2375-2387. DOI:10.3168/jds.S0022-0302(04)73359-7 |
| [12] |
TORSHIZI M E. Effects of season and age at first calving on genetic and phenotypic characteristics of lactation curve parameters in Holstein cows[J]. Journal of Animal Science and Technology, 2016, 58: 8. DOI:10.1186/s40781-016-0089-1 |
| [13] |
OLORIA V E, BROTHERSTONEA S, HILLA W G, et al. Fit of standard models of the lactation curve to weekly records of milk production of cows in single herd[J]. Livestock Production Science, 1999, 58(1): 55-63. DOI:10.1016/S0301-6226(98)00194-8 |
| [14] |
毛永江, 张美荣, 许兆君, 等. 用Wood模型拟合南方中国荷斯坦牛产奶量、乳脂率、乳蛋白率和体细胞评分及其效果分析[J]. 畜牧兽医学报, 2012, 43(12): 1904-1909. |
| [15] |
熊本海, 杨亮, 杨琴, 等. 中国北方荷斯坦奶牛乳产量及乳成分变化的普适模型构建[J]. 畜牧兽医学报, 2014, 45(12): 1939-1948. |
| [16] |
FRIGGENS N C, EMMANS G C, KYRIAZAKIS I, et al. Feed intake relative to stage of lactation for dairy cows consuming total mixed diets with a high or low ratio of concentrate to forage[J]. Journal of Dairy Science, 1998, 81(8): 2228-2239. DOI:10.3168/jds.S0022-0302(98)75802-3 |
| [17] |
张美荣, 廖想想, 陈丹, 等. 产犊季节、胎次及牛场对荷斯坦牛泌乳性能的影响[J]. 中国牛业科学, 2012, 38(4): 6-9. |
| [18] |
罗清尧, 熊本海, 马毅, 等. 中国荷斯坦奶牛第二泌乳期泌乳曲线模型的研究[J]. 中国农业科学, 2010, 43(23): 4910-4916. DOI:10.3864/j.issn.0578-1752.2010.23.017 |
| [19] |
STERI R, CAPPIO-BORLINO A, MACCIOTTA N P P. Modelling extended lactation curves for milk production traits in Italian Holsteins[J]. Italian Journal of Animal Science, 2009, 8(2S): 165-167. |
| [20] |
GOŁEBIEWSKI M, BRZOZOWSKI P, GOŁEBIEWSKI L. Analysis of lactation curves, milk constituents, somatic cell count and urea in milk of cows by the mathematical model of Wood[J]. Acta Veterinaria Brno, 2011, 80(1): 73-80. DOI:10.2754/avb201180010073 |




